Pitágoras y su famoso teorema

EL ÁGORA DE THALES

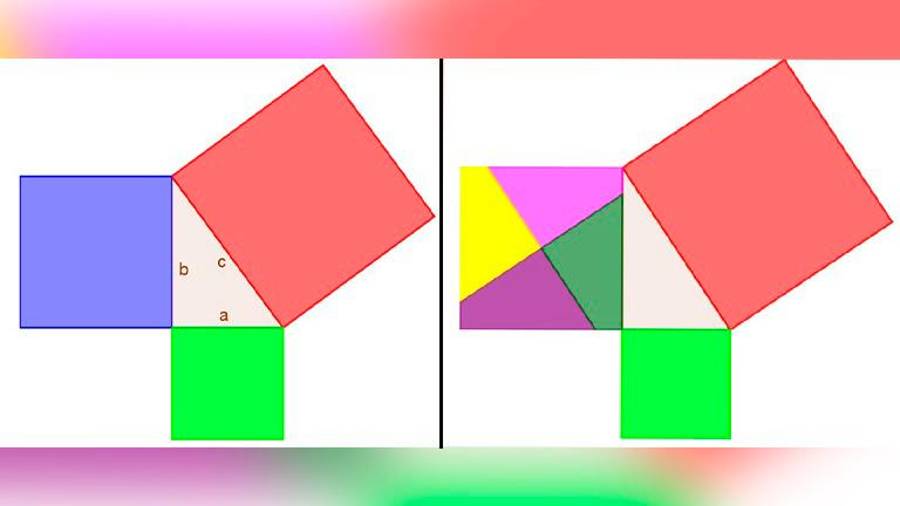
Quizás recordemos la primera vez que escuchamos el teorema de Pitágoras, lo normal sería que esto ocurriera en la escuela, aunque si vimos la película “El mago de Oz” dirigida en 1939 por Víctor Fleming, puede que nos suene lo que decía el espantapájaros “la suma de la raíz cuadrada de cada uno de los lados de un triángulo rectángulo es igual a la raíz cuadrada del otro lado”, añadiendo además que por fin tiene cerebro. En realidad este no es el teorema de Pitágoras, puede que el espantapájaros estuviera mal asesorado y lo recitó de manera incorrecta. El teorema de Pitágoras establece que en un triángulo rectángulo, recordemos que es un triángulo en el que dos de sus lados, llamados catetos forman un ángulo recto (90 grados), la suma de los cuadrados de las medidas de estos lados es igual al cuadrado de la medida del otro lado que recibe el nombre de hipotenusa. Si a y b son los catetos del triángulo, y c es la hipotenusa, el teorema de Pitágoras no dice que a2 + b2 = c2. Existe una gran cantidad de demostraciones de este teorema, más de trescientas. A partir de algunas de ellas se pueden construir un puzle para completar el cuadrado de color rojo con las piezas en las que se dividen los cuadrados azul y verde. De esta forma se puede comprobar que la suma de los cuadrados de lados a y b es igual al cuadrado del lado c. En la segunda figura con las cuatro piezas en las que se ha dividido el cuadrado azul y con el cuadrado verde hay que completar el cuadrado rojo. Basta buscar en Internet para encontrar algunas de estas demostraciones.

A Pitágoras, matemático griego (570 a.C. – 490 a.C.) se le atribuye el descubrimiento de este teorema, aunque hay pruebas que confirman que este teorema ya era conocido alrededor del 800 a.C. por el matemático hindú Baudhayana, incluso hay teorías que indican que era conocido incluso por los babilonios. Este teorema identifica a un tipo determinado de triángulos, denominados pitagóricos que son triángulos rectángulos, por tanto se cumple dicho teorema, pero cuyos lados sean números naturales. Por ejemplo el triángulo de lados 3, 4 y 5 es un triángulo pitagórico ya que 32+42=52, siendo por tanto 3 y 4 las medidas de los catetos y 5 la medida de la hipotenusa. Encontrar ternas que cumplan esta condición ha sido un reto para muchos matemáticos a lo largo de la historia, por lo que animamos al lector a encontrar alguno, de las que existen dieciséis cuyos lados son menores que 100. Como curiosidad la terna 3, 4 y 5 es la única de las anteriores cuyos lados son números consecutivos y también el único que su perímetro (suma de los tres lados 3+4+5=12, es el doble de su área que es 6.

En las figuras aparece el triángulo rectángulo y los cuadrados dibujados sobre cada uno de los lados, de manera que la suma de las áreas de los cuadrados dibujados sobre los catetos es igual al área del cuadrado dibujado sobre la hipotenusa, tal y como establece el famoso teorema de Pitágoras, que se puede generalizar dibujando otros polígonos regulares sobre cada uno de los lados ya que la relación se mantiene. Así si dibujamos un triángulo equilátero o cualquier otro polígono regular, la suma de las áreas de los polígonos dibujados sobre los catetos es igual al área de la figura dibujada sobre la hipotenusa. Y aún más, si dibujamos semicírculos también se verifica. Animamos al lector a probar con otras figuras y sobre todo a construir algún nuevo rompecabezas con las distintas demostraciones de este teorema que podrá encontrar en la Web.

(*) Agustín Carrillo de Albornoz Torres, de la Sociedad Andaluza de Educación Matemática Thales.

Actividad subvencionada por la Diputación Provincial de Jaén.